from catsim.cat import generate_item_bank
from catsim.initialization import FixedPointInitializer
from catsim.selection import RandomesqueSelector
from catsim.estimation import NumericalSearchEstimator
from catsim.stopping import MaxItemStopper
from catsim.simulation import Simulator
import numpy as np
import pandas as pdOverview
In this post, we’ll explore how to perform item analysis on cognitive assessment items, focusing on generating an item bank and simulating responses. We will examine the difficulty and discrimination parameters of the items. The results from these analyses will help determine whether the items are suitable for specific purposes, such as recruitment assessments.

Setting Up the Simulation
To ensure repeatable results, we’ll use numpy to set a random seed. The item bank will be based on the 1-Parameter Logistic (1PL) model, which allows item difficulty to vary, while the discrimination parameter remains constant across items. In this way, we assume that all items are equally capable of distinguishing between high- and low-ability individuals.
All individuals in the simulation start with an initial ability estimate of 0. When selecting an item, given the current ability estimate, we will use a randomesque selector. This method first identifies a set of items that are most representative for the current ability estimate, then randomly selects one item from this subset. In our case, we will choose five representative items and randomly select one from that group. This approach is advantageous because it helps reduce item overexposure in real-world scenarios. Each respondent’s simulation will terminate after 20 items, though in practice, the stopping rule may include other criteria such as a standard error threshold or a combination of item count and standard error.
# Set seed to ensure repeatable results
np.random.seed(1909)
# Generate a 300 item bank using the 1-Parameter Logistic Model
item_bank = generate_item_bank(300, "1PL")
# Setup CAT using an initial fixed point theta estimate, the randomesque item selector, the numerical search estimator, and the termination criteria
initial_ability = FixedPointInitializer(start=0)
item_selection = RandomesqueSelector(bin_size=5)
estimate_ability = NumericalSearchEstimator()
max_item_stop = MaxItemStopper(20)
# Setup simulation using generated item bank and 4000 respondents
sim = Simulator(items=item_bank, examinees=4000)
# Run simulation
(
sim
.simulate(
initializer=initial_ability,
selector=item_selection,
estimator=estimate_ability,
stopper=max_item_stop)
)
# For each respondent, merge administered items and the associated responses (whether the response was correct or not)
simulation_results = zip(sim.administered_items, sim.response_vectors)
# Concatenate respondent results into a DataFrame
simulation_results = (
pd
.concat([
pd.DataFrame(data=[response_correct], columns=item_number)
for item_number, response_correct
in simulation_results])
.reset_index(drop=True)
)
# Rename DataFrame columns to clarify meaning
item_bank_simulation = pd.DataFrame(sim.items)
item_bank_simulation = item_bank_simulation.rename(
columns={
0: "item_discrimination",
1: "item_difficulty",
2: "pseudo_guessing",
3: "upper_asymptote",
4: "item_exposure"})Item Easiness
With a set of responses, most would turn to Item Response Theory (IRT) to estimates parameters such as item difficulty. However, a simpler alternative is to calculate the pass rates for each item. While referred to as Item Difficulty in IRT, what we’re actually measuring here is Item Easiness, which ranges from 0 to 1. Table 1 shows the generated parameters for our item bank. Again, we only estimated item difficulty, all remaining parameters were fixed. The last two columns in the table display the exposure rate (how often an item was shown to respondents) and the manually calculated easiness.
For example, the first row in Table 1 shows an item with an estimated difficulty of -.62, an exposure rate of 5%, and an easiness of 59%. From the difficulty perspective, this item is relatively easy, as indicated by the fact that 59% of respondents answered it correctly. Additionaly, the item was shown to approximately 5% of the total respondents (~200 individuals).
In contrast, the second row of Table 1 presents an item with a difficulty estimate of .69, an exposure rate of 11%, and an easiness of 46%. This item is more difficult, as evidenced by the lower percentage of respondents answering it correctly.
item_easiness = simulation_results.mean(axis=0)
item_easiness.name = "easiness"
item_bank_simulation = (
item_bank_simulation
.merge(
item_easiness,
left_index=True,
right_index=True)
)library(ggplot2)
library(kableExtra)
library(reticulate)
library(scales)py$item_bank_simulation |>
head(10) |>
kbl() |>
kable_minimal()| item_discrimination | item_difficulty | pseudo_guessing | upper_asymptote | item_exposure | easiness |
|---|---|---|---|---|---|
| 1 | -0.6168792 | 0 | 1 | 0.05325 | 0.5868545 |
| 1 | 0.6891809 | 0 | 1 | 0.10575 | 0.4562648 |
| 1 | 0.0893915 | 0 | 1 | 0.04375 | 0.5371429 |
| 1 | 1.3452045 | 0 | 1 | 0.16175 | 0.3477589 |
| 1 | 0.5316801 | 0 | 1 | 0.08300 | 0.4277108 |
| 1 | 0.3823903 | 0 | 1 | 0.03225 | 0.503876 |
| 1 | -0.0650143 | 0 | 1 | 0.05625 | 0.5066667 |
| 1 | -0.6844640 | 0 | 1 | 0.05250 | 0.6333333 |
| 1 | 0.6673186 | 0 | 1 | 0.10400 | 0.4134615 |
| 1 | -1.2625439 | 0 | 1 | 0.06400 | 0.609375 |
For comparative purposes, Figure 1 illustrates the relationship between the initially generated item difficulty and the manually calculated easiness. As shown, the two values are highly correlated. Additionally, most of items fall within one standard deviation of the mean, indicating that there are few items that are either extremely easy or extremely difficult. While excessively easy items are generally undesirable in most testing contexts, having too few difficult items could hinder the accurate estimation of ability.
py$item_bank_simulation |>
ggplot(aes(x = as.numeric(item_difficulty), y = as.numeric(easiness))) +
geom_jitter(
alpha = .6,
colour = "#532473",
fill = "#F06BF2",
shape = 21,
stroke = 1
) +
geom_smooth(
colour = "#04588C",
method = "lm",
se = F) +
labs(
x = "Simulated Item Difficulty",
y = "Item Easiness"
) +
scale_x_continuous(
limits = c(-4, 4)
) +
scale_y_continuous(
limits = c(0, 1),
labels = label_percent()
) +
theme_minimal()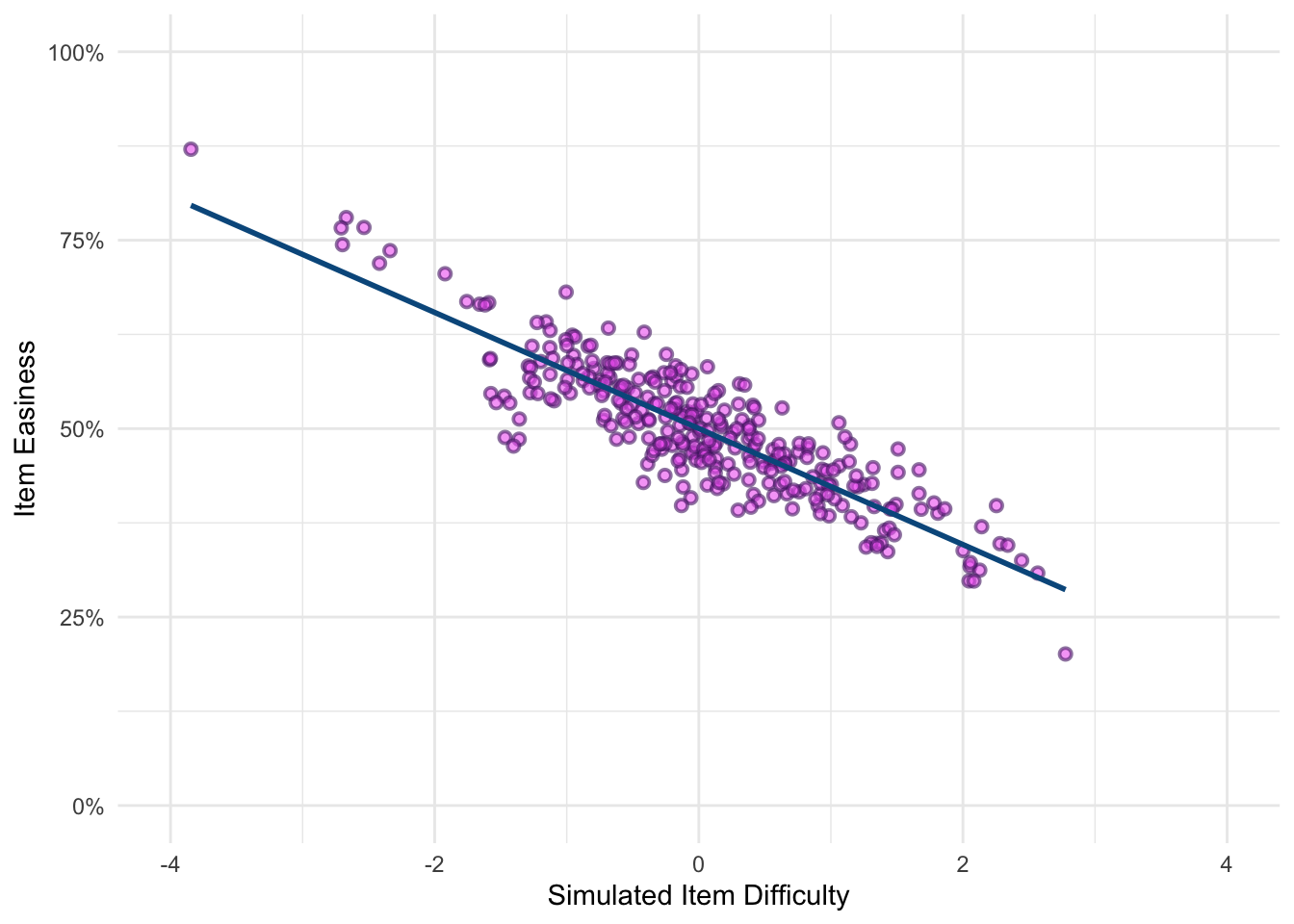
Item Discrimination
Ideally, we want our items to effectively differentiate between individuals with high and low ability. If an item fails to do this, we may need to question its utility within the item bank. Since we used the 1-PL model to generate the item bank, item discrimination was not estimated as part of the model. However, we can calculate it using the following steps:
Calculate the total score for each respondent across the 20 items.
Split the respondents into two groups: a higher-ability group and a lower-ability group. While experts often suggest using the top and bottom 27%, in this case, we use the top and bottom quartiles.
For each item, calculate the pass rate in both the higher- and lower-ability groups.
Subtract the pass rate of the lower group from the pass rate of the higher group to calculate the discrimination index.
A well-discriminating item should have a higher pass rate in the high-ability group compared to the low ability group. Thus, a discrimination value close to 1 is ideal, while a value close to 0 indicates poor discrimination. If an item to performs better in the low-scoring group, it can be considered problematic. A general rule of thumb is that items should have a discrimination index of at least .3 to be considered effective.
simulation_results["total_score"] = simulation_results.sum(axis=1)
simulation_results["score_group"] = pd.qcut(simulation_results["total_score"], 4, labels=False)
item_discrimination = (
simulation_results
.groupby("score_group")
.mean()
.filter(items=[0,3], axis=0) # Take the bottom and top performing groups only
.diff()
.drop(columns=["total_score"])
.iloc[1]
)
item_discrimination.name = "discrimination"
item_bank_simulation = (
item_bank_simulation
.merge(
item_discrimination,
right_index=True,
left_index=True)
)
good_discrimination_items = item_discrimination.astype("float").nlargest(5)
poor_discrimination_items = item_discrimination.astype("float").nsmallest(5)
good_discrimination_items = item_bank_simulation.iloc[good_discrimination_items.index]
poor_discrimination_items = item_bank_simulation.iloc[poor_discrimination_items.index]Table 2 shows the top five items based on their discrimination index. For each of these items, the discrimination index exceeds .3, indicating that the high-ability group performs better on these items than lower-ability group. Additionally, most of the easiness values hover around 50%, which is where we would expect the majority of individuals to be.
py$good_discrimination_items |>
kbl() |>
kable_minimal()| item_discrimination | item_difficulty | pseudo_guessing | upper_asymptote | item_exposure | easiness | discrimination |
|---|---|---|---|---|---|---|
| 1 | -0.2857401 | 0 | 1 | 0.04375 | 0.48 | 0.5336134 |
| 1 | -1.4031805 | 0 | 1 | 0.10800 | 0.4768519 | 0.5114439 |
| 1 | 2.4441997 | 0 | 1 | 0.06000 | 0.325 | 0.5008215 |
| 1 | -1.3605601 | 0 | 1 | 0.09775 | 0.4859335 | 0.4945513 |
| 1 | -1.2912622 | 0 | 1 | 0.08575 | 0.5830904 | 0.4870968 |
Table 3 presents the bottom five items based on their discrimination index. In these cases, the lower-ability group actually performs better than the high-ability group, which raises concerns. Ideally, higher-ability respondents should outperform lower-ability ones on these items. These items would likely require review or potential removal from the item bank.
py$poor_discrimination_items |>
kbl() |>
kable_minimal()| item_discrimination | item_difficulty | pseudo_guessing | upper_asymptote | item_exposure | easiness | discrimination |
|---|---|---|---|---|---|---|
| 1 | -0.0163783 | 0 | 1 | 0.24075 | 0.5233645 | -0.3861653 |
| 1 | 0.0114132 | 0 | 1 | 0.23300 | 0.5 | -0.3607507 |
| 1 | 0.0072161 | 0 | 1 | 0.23100 | 0.495671 | -0.3093596 |
| 1 | 0.0204674 | 0 | 1 | 0.23450 | 0.4552239 | -0.306629 |
| 1 | 0.0182604 | 0 | 1 | 0.23075 | 0.531961 | -0.2364526 |
Summary
In this post, we’ve demonstrated how item analysis can be applied to cognitive assessment tems, focusing on both easiness and discrimination. This approach is valuable not only for constructing new items but also for evaluating an established item bank. Additionally, it provides a straightforward method for assessing item performance without relying on more complex IRT models.