library(data.table)
library(ggplot2)
library(jsonlite)
library(rmarkdown)
library(themis)
library(tidymodels)
library(vip)Psychometric data is collected for various reasons. In some cases, it is used to describe an individual (e.g., to understand their learning strategies). Whereas, in others it is used for predictive purposes, which is what we attempt here. Using data from Kaggle, we look at whether we can accurately predict employee wellbeing using psychometric data.
Our Data
There are two files: the metadata regarding the questionnaire and the responses to the questionnaire itself.
The metadata is in a JSON format so we use lapply to iterate over and transform the data into a rectangular format. For responses, we leave as is, but add an index value as this will come in handy for melting the data into a long format.
# Tidy JSON Meta Data -----------
questionnaire_meta_data <-
read_json("data/questionnaire_schema.json")
questionnaire_meta_data <-
lapply(questionnaire_meta_data, function(x) {
item_answers <- x$answers
item_answers <- lapply(item_answers, as.data.table) |>
rbindlist() |>
setnames(old = "text",
new = "value",
skip_absent = TRUE)
data.table(
item_label = x$position,
item_text = x$text,
item_answer_position = item_answers$position,
item_answer_value = item_answers$value
)
}) |>
rbindlist()
# Read Questionnaire Responses -------
questionnaire_responses <-
fread("data/retail_chain_salespeople_engagement.csv")
# Add Index Variable -----------------
questionnaire_responses[, index := 1:nrow(questionnaire_responses)]paged_table(questionnaire_meta_data)Survey Completion Time
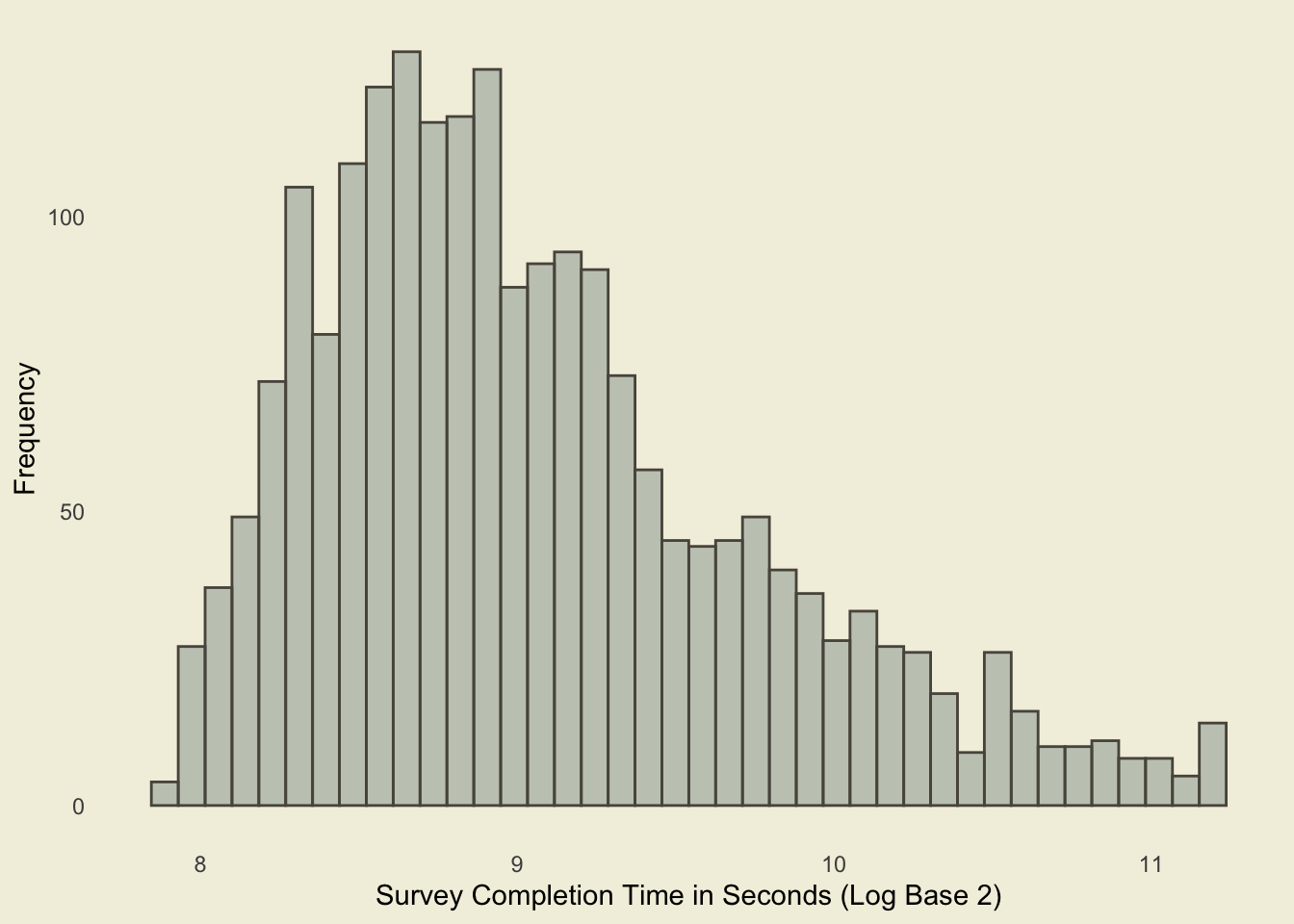
Survey completion was recorded in seconds. On average, respondents spent 482 seconds (Minimum Time: 241 seconds; Maximum Time: 2386 seconds) completing the survey. This equates to around an average item completion rate of 7.65 seconds. For visualisation purposes, we transform the values using Log Base 2 (Figure 1). Taking both the visualisation and descriptive statistics, we can see that there aren’t substantial outliers with regards to survey completion times.
questionnaire_responses[, time := log2(time)]
questionnaire_responses |>
ggplot(aes(x = time)) +
geom_histogram(
alpha = .4,
fill = "#798C8C",
colour = "#59554C",
bins = 40
) +
theme(
panel.grid = element_blank(),
panel.background = element_rect(
fill = "#F2EFDF",
colour = "#F2EFDF"
),
plot.background = element_rect(
fill = "#F2EFDF",
colour = "#F2EFDF"
),
axis.ticks = element_blank()
) +
labs(
x = "Survey Completion Time in Seconds (Log Base 2)",
y = "Frequency"
)
Predictor Variables
Respondents were asked to provide responses to 60 binary items designed to measure personality. For example:
| Item | Option One | Option Two |
|---|---|---|
| Being in a company you usually | Join the conversation | Talk with each separately |
In other words, the respondent is asked to select an option from the pair that represents them well.
Outcome Variables
The survey contained three outcome variables measured by the following items:
How much do you like what you are doing at work now?
I would recommend our Company as a good place to work to my friends and acquaintances.
My work gives me a sense of fulfillment.
The metadata suggests to re-score the data with the negative response being of a high value, whilst the positive response is assigned a low value. Here, we do the opposite (positive responses are given a high value; negative responses are given a low value).
# Re-code the item: How much do you like what you are doing at work now? Reverse scored too.
questionnaire_responses[,
q61 := fcase(
q61 == -100, 1, # Do not like
q61 == -33, 2,
q61 == 34, 3,
q61 == 100, 4. # Very like
)]
# Re-code the item: I would recommend our Company as a good place to work to my friends and acquaintances. Reverse scored too.
questionnaire_responses[,
q62 := fcase(
q62 == -100, 1,
q62 == -80, 2,
q62 == -60, 3,
q62 == -40, 4,
q62 == -20, 5,
q62 == 0, 6,
q62 == 20, 7,
q62 == 40, 8,
q62 == 60, 9,
q62 == 80, 10,
q62 == 100, 11
)]
# Re-code the item: My work gives me a sense of fulfillment. Reverse scored too.
questionnaire_responses[,
q63 := fcase(
q63 == -100, 1,
q63 == -50, 2,
q63 == 0, 3,
q63 == 50, 4,
q63 == 100, 5
)]Figure 2 presents the frequency of each response option across the three outcome variables. The frequencies have been faceted by the recorded position, of which there are two: Point of Sales Manager and Specialist.
From the distributions, we can see that respondents have a positive view of the company:
They tend to enjoy what they’re doing at work.
They seem to feel fulfilled by their work.
They would recommend the company as a good place to work.
outcome_variable_long <-
questionnaire_responses[,
.(index, position, q61, q62, q63)] |>
melt(
id.vars = c("index", "position"),
variable.name = "item_name",
value.name = "response_value"
)
outcome_variable_long[,
item_name := fcase(
item_name == "q61",
"Enjoy Work",
item_name == "q62",
"Recommend",
item_name == "q63",
"Fulfillment"
)]
outcome_variable_long[,
position := ifelse(position == 1,
"Point of Sales Manager",
"Specialist")]
outcome_variable_long |>
ggplot(aes(x = response_value)) +
stat_count(alpha = .4,
fill = "#798C8C",
colour = "#59554C") +
facet_grid(
position ~ item_name,
scales = "free_x") +
theme(
axis.ticks = element_blank(),
panel.grid = element_blank(),
panel.background = element_rect(fill = "#F2EFDF",
colour = "#F2EFDF"),
plot.background = element_rect(fill = "#F2EFDF",
colour = "#F2EFDF"),
strip.background = element_rect(fill = "#F2EFDF",
colour = "#59554C")
) +
scale_x_continuous(
breaks = 1:11*1
) +
labs(x = "Response Option",
y = "Frequency")
For model building, we select one outcome variable: “Do you like what you are doing at work now?” I selected this because I felt it was a good overall evaluation of how an individual feels about their current employer.
Work Enjoyment Model
Our aim is to predict respondent enjoyment of work based on the 60 self-assessment items they were presented with. The outcome variable is a factor with four levels:
Do Not Like
Rather Don’t Like It
Rather Like It
Very Like
Given this, we will use multinomial classification through the use of a Random Forest model.
# Buid a Workflow to Model Work Enjoyment
questionnaire_responses[,
q61 := as.factor(fcase(
q61 == 1, "Do Not Like",
q61 == 2, "Rather Don't Like It",
q61 == 3, "Rather Like It",
q61 == 4, "Very Like"
))]
work_enjoyment_data <-
questionnaire_responses[, c(1:61, 64)]First, we setup our workflow and add our model. As above, we are using the Random Forest model for our multinomial classification.
# Model Workflow
work_enjoyment_wf <-
workflow()
# Setup Model Used
random_forest_model <-
rand_forest(trees = 1e3, min_n = 5) |>
set_engine("ranger") |>
set_mode("classification")
work_enjoyment_wf <-
work_enjoyment_wf |>
add_model(random_forest_model)Next we specify the recipe and pre-processing steps of the workflow. The model is straightforward, we’re predicting work enjoyment based on the 60 self-assessment items. As shown in Figure 2, most respondents selected option 3; the classes aren’t balanced. Therefore, we use the SMOTE algorithm to over-sample the minority classes. Put simply, SMOTE generates synthetic data based on the minority class (e.g., Do Not Like it responses) in order to make the classes balanced.
# Define Predictor Variables and Outcome Variable
work_enjoyment_preprocess <-
recipe(q61 ~ ., data = work_enjoyment_data) |>
step_smote(q61)
work_enjoyment_wf <-
work_enjoyment_wf |>
add_recipe(work_enjoyment_preprocess)For training, we use cross-validation. Specifically, we use repeated v-fold cross-validation wherein we repeat the cross-fold validation with a view of obtaining a more reliable estimate.
# Split into Training and Test Data
work_enjoyment_split <- initial_split(work_enjoyment_data)
work_enjoyment_train <- training(work_enjoyment_split)
work_enjoyment_test <- testing(work_enjoyment_split)
work_enjoyment_folds <-
vfold_cv(
work_enjoyment_train,
v = 10,
repeats = 10)
work_enjoyment_results <-
work_enjoyment_wf |>
fit_resamples(
work_enjoyment_folds,
control = control_resamples(save_pred = T))Work Enjoyment Model Results
Let’s see how our model performed with regards to predicting work enjoyment.
Our accuracy is a little of 50%, which means that our model is slightly better than a random guess.
work_enjoyment_results |>
collect_metrics()# A tibble: 2 × 6
.metric .estimator mean n std_err .config
<chr> <chr> <dbl> <int> <dbl> <chr>
1 accuracy multiclass 0.552 100 0.00314 Preprocessor1_Model1
2 roc_auc hand_till 0.675 100 0.00330 Preprocessor1_Model1We can use the confusion matrix of predictions to see where the model predicts outcomes well. Based on our training data, we can see that it does well in predicting “Rather Like It”. This is the biggest class we have and even after using the SMOTE algorithm, “Rather Like It” remains the easiest class to predict.
work_enjoyment_results |>
collect_predictions() |>
conf_mat(q61, .pred_class) Truth
Prediction Do Not Like Rather Don't Like It Rather Like It
Do Not Like 61 37 67
Rather Don't Like It 44 115 238
Rather Like It 821 2459 7784
Very Like 34 39 521
Truth
Prediction Very Like
Do Not Like 3
Rather Don't Like It 28
Rather Like It 2750
Very Like 709Last Fit
Based on the training data, we know the model is far from good, on par with flipping a coin.
At this point, you would test other models, as opposed to a single model. We would even explore tuning hyperparameters. However, we’re sticking with the Random Forest model.
Tidymodels makes it straightforward in applying the workflow to the test data using the last fit function. As we don’t have separate models, we just apply the Random Forest.
As expected, the model is little better than a random guess. Therefore, I wouldn’t be using this model to predict employee wellbeing.
last_fit_results <-
work_enjoyment_wf |>
last_fit(work_enjoyment_split)
last_fit_results |>
collect_metrics()# A tibble: 2 × 4
.metric .estimator .estimate .config
<chr> <chr> <dbl> <chr>
1 accuracy multiclass 0.592 Preprocessor1_Model1
2 roc_auc hand_till 0.658 Preprocessor1_Model1Conclusion
Accurately predicting employee happiness was not achieved. The model was slightly better than a random guess. There are various reasons. Not all the personality variables may be relevant to understanding evaluations of an employer. Moreover, work enjoyment is likely to fluctuate within and across days, and this variability may be associated with factors within the workplace environment. It is still important, however, to test different models to see if improvements in accuracy could be improved.