Alex Wainwright - Good Fit, Fragile Inference

Introduction

Structural equation models are commonly used in the self-regulated learning (SRL) literature to relate latent psychological constructs to academic performance. These models often appear technically sophisticated and theoretically grounded, yet their conclusions rest heavily on strong measurement assumptions and are frequently estimated using small, highly selected samples. As a result, apparent model fit can obscure more fundamental problems in specification and inference.

This post examines one such model from Bernacki et al. (2023), focusing not on the substantive SRL theory but on the statistical structure of the analysis. In particular, it evaluates the treatment of exam performance as a latent variable and the downstream implications for the reported structural relations. The central premise is straightforward: if the measurement model is unstable or implausible, any conclusions drawn from the structural paths are necessarily fragile.

Rather than proposing an alternative model or re-analysing the original data, I use the summary statistics reported in the paper to simulate the behaviour of the authors’ specified models under repeated sampling. This allows an assessment of model fit, residual structure, and parameter stability given the reported sample size and covariance structure.

The aim is therefore limited and methodological. I do not challenge the theoretical relevance of SRL constructs, nor do I claim that different modelling choices would necessarily lead to stronger results. Instead, the analysis highlights how small samples, weak measurement, and conditional independence assumptions interact to produce results that appear more robust than the data can reasonably support.

Code

# Libraries ---------------------------
library(data.table)
library(flextable)
library(ggplot2)
library(lavaan)
library(MASS)

set.seed(1225)

flowchart LR
    %% Observed Predictors (Rectangles)
    D[Declarative SRL]
    C[Conceptual SRL]
    A[Application SRL]

    %% Latent Factor (Stadium/Ellipse shape)
    EX([EXAM latent])

    %% Observed Indicators (Rectangles)
    E2[Exam 2]
    E3[Exam 3]
    E4[Exam 4]

    %% Structural paths (Predictors to Latent)
    D --> EX
    C --> EX
    A --> EX

    %% Measurement model (Latent to Indicators)
    EX --> E2
    EX --> E3
    EX --> E4

Code

# Study One Parameters ----------------
# Variable Names
var_names <- c("Exam_2", "Exam_3", "Exam_4", "Module_1", "Module_2", "Module_3")

# Means
means <- c(84.61, 70.30, 75.12, 54.96, 77.85, 82.54)
names(means) <- var_names

# Standard Deviations
sds <- c(11.43, 22.58, 22.24, 42.17, 14.05, 19.74)
names(sds) <- var_names

# Empty matrix
cor_matrix <- matrix(1, nrow = 6, ncol = 6)
colnames(cor_matrix) <- rownames(cor_matrix) <- var_names

# Filling with correlation values
cor_matrix[2, 1] <- 0.738
cor_matrix[3, 1:2] <- c(0.612, 0.692)
cor_matrix[4, 1:3] <- c(0.570, 0.489, 0.392)
cor_matrix[5, 1:4] <- c(-0.101, -0.137, -0.082, -0.014)
cor_matrix[6, 1:5] <- c(0.590, 0.405, 0.513, 0.438, 0.223)

cor_matrix[upper.tri(cor_matrix)] <- t(cor_matrix)[upper.tri(cor_matrix)]

cov_matrix <- diag(sds) %*% cor_matrix %*% diag(sds)

Exam Performance as a Latent Variable

Scores were recorded across four exams. For Model 4 (Study One), only Exams 2, 3, and 4 were included in the measurement model. Exams 2 and 3 were within-module tests, whereas Exam 4 was a cumulative final assessment. The authors specify a reflective measurement model in which a single latent variable underlies performance across these three exams. Under this specification, variation in exam scores is assumed to arise from a common latent cause, such that a unit change in the latent variable would lead to systematic increases or decreases in each observed exam score.

This specification is problematic for several reasons. First, a reflective measurement model assumes conditional (local) independence of the indicators given the latent variable. This assumption is implausible in the present context. The exams are temporally ordered, such that performance on later exams is partially a function of performance on earlier exams through feedback, learning, and strategic adjustment. Consequently, residual dependence between exam scores is expected even after conditioning on any putative latent factor.

Second, the exams are not exchangeable indicators. Exams 2 and 3 assess distinct instructional units, while Exam 4 is cumulative by design. Substantial content overlap is therefore inevitable, particularly between the final exam and preceding assessments. This further violates the assumption that the observed covariance among exam scores can be attributed solely to a single latent construct rather than to shared content and instructional sequencing.

Taken together, these considerations imply that the proposed measurement model is misspecified. Any apparent model fit is therefore likely to reflect the flexibility of the CFA under small sample conditions rather than evidence for a substantively meaningful latent exam performance construct.

Simulation Results

When specified without constraints, a one-factor measurement model for three exam scores is just-identified and therefore untestable. To enable model evaluation, we impose tau-equivalence, constraining all factor loadings to be equal, and fix the latent factor variance to one. This yields an overidentified model with positive degrees of freedom, allowing assessment of model fit.

Using the reported means, standard deviations, and correlations from Study One, we simulated 1,000 datasets of size n=49. For each replication, exam scores were generated from a multivariate normal distribution and truncated to the observed percentage range [0,100]. The constrained measurement model was then fitted using robust maximum likelihood estimation.

Code

mm_warning <- 0

measurement_model_fit <- lapply(1:1e3, function(idx) {
  tryCatch(
    expr = {
      study_one_sim <- mvrnorm(n = 49, mu = means, Sigma = cov_matrix)
      
      study_one_sim <- pmax(pmin(study_one_sim, 100), 0)
      
      measurement_model <- "
        Exam_Score ~~ 1*Exam_Score
        Exam_Score =~ a*Exam_2 + a*Exam_3 + a*Exam_4
      "
      
      mm_results <- cfa(
        measurement_model,
        data = as.data.frame(study_one_sim),
        estimator = "MLR",
        std.lv = T
      )
      
      mm_resid <- resid(mm_results, type = "cor")$cov
      mm_resid <- as.data.table(mm_resid[lower.tri(mm_resid)])
      
      mm_fit <- fitmeasures(mm_results,
                            c(
                              "chisq.scaled",
                              "cfi.robust",
                              "tli.robust",
                              "rmsea.robust"
                            )) |>
        as.data.table(keep.rownames = T)
      
      setnames(mm_fit, new = c("Fit Measure", "Value"))
      mm_fit[, `Fit Measure` := fcase(
        `Fit Measure` == "chisq.scaled",
        "Chi-Square",
        `Fit Measure` == "cfi.robust",
        "CFI",
        `Fit Measure` == "tli.robust",
        "TLI",
        `Fit Measure` == "rmsea.robust",
        "RMSEA"
      )]
      
      return(list(residuals = mm_resid, model_fit = mm_fit))
    },
    warning = function (w) {
      mm_warning <<- mm_warning + 1
      return(NULL)
    },
    error = function (e) {
      return(NULL)
    }
  )
})

Code

measurement_model_residuals <-
  Filter(Negate(is.null), lapply(measurement_model_fit, function (x) x$residuals)) |>
  rbindlist() 

measurement_model_residuals[, idx := rep(1:3, length.out = nrow(.SD))]

measurement_model_residuals <-
  measurement_model_residuals[, .(
    Mean = mean(V1),
    SD = sd(V1)
  ), by = idx]

measurement_model_residuals[, "Item ID One" := c("Item One", "Item One", "Item Two")]
measurement_model_residuals[, "Item ID Two" := c("Item Two", "Item Three", "Item Three")]

measurement_model_residuals[, idx := NULL]

measurement_model_residuals[, .(`Item ID One`, `Item ID Two`, Mean, SD)] |>
  as_flextable() |>
  colformat_double(digits = 3) |>
  align_nottext_col(align = "center")

Item ID One	Item ID Two	Mean	SD
character	character	numeric	numeric
Item One	Item Two	0.115	0.038
Item One	Item Three	-0.002	0.057
Item Two	Item Three	0.330	0.091
n: 3

Across 340 successful replications without negative variances (out of 1,000 attempted), global fit indices exhibited substantial variability. While acceptable fit was obtained in some samples, equally plausible samples generated poor fit, and residual correlations remained non-negligible. This instability indicates that apparent model fit is highly sensitive to sampling variation rather than reflective of a stable underlying measurement structure.

Code

Filter(Negate(is.null), lapply(measurement_model_fit, function (x) x$model_fit)) |>
  rbindlist() |>
  ggplot(aes(Value)) +
  geom_histogram(colour = "black", fill = "white") +
  facet_wrap(~`Fit Measure`, scales = "free_x") +
  theme_bw()

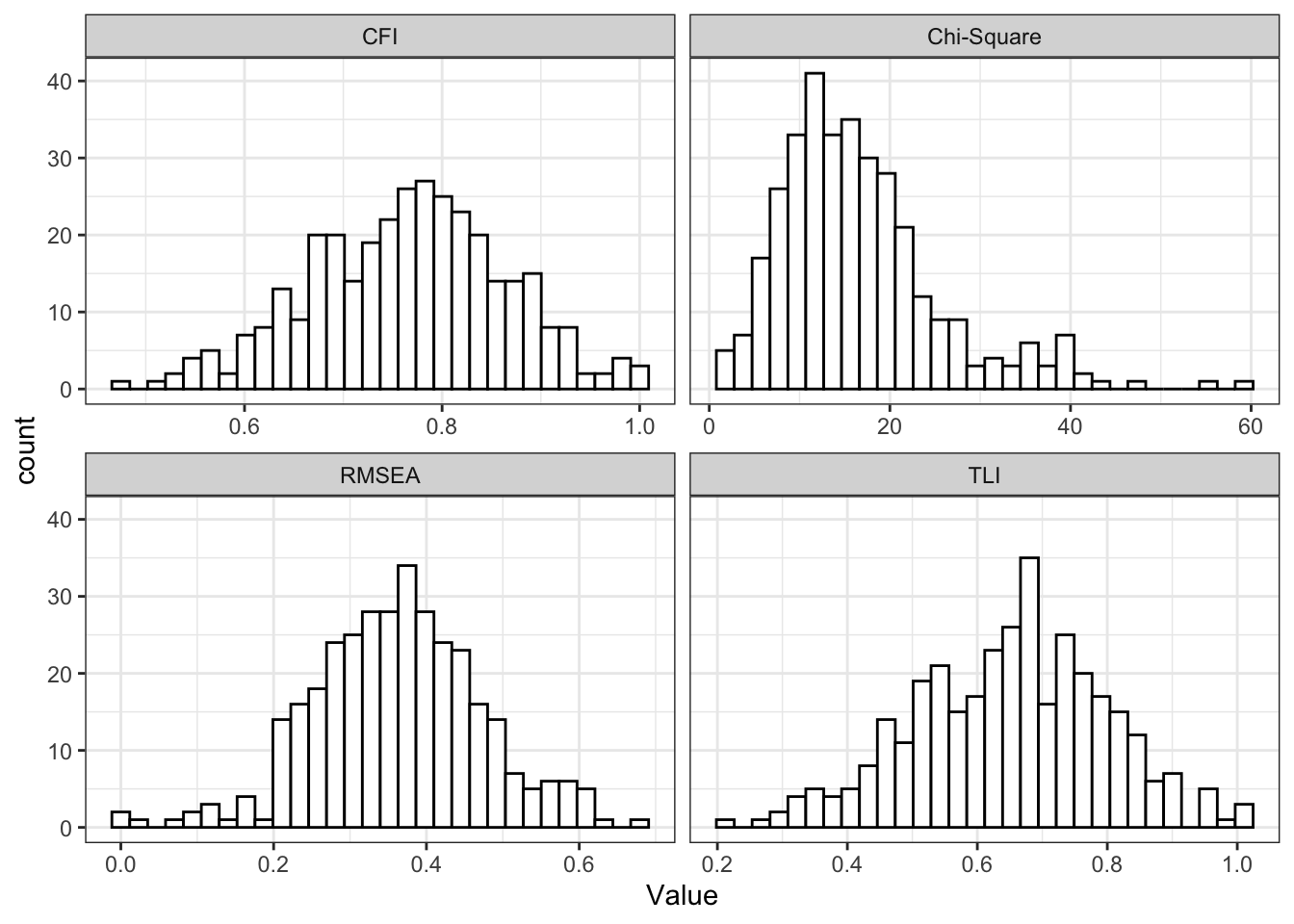
Taken together, these results suggest that the proposed measurement model lacks robustness at the given sample size. Any inference drawn from the latent exam factor is therefore contingent on strong and empirically unsupported assumptions, undermining its use as a foundation for subsequent structural path analyses.

Exam Performance: Structural Model

The results above indicate that the proposed measurement model for exam performance is unstable and likely misspecified. In principle, this undermines the interpretability of any subsequent structural relations. Nevertheless, to assess whether the authors’ substantive conclusions are robust even under their preferred specification, we proceed by conditionally accepting the measurement model and examining the behaviour of the structural paths.

Simulation Results

Using the same simulation framework as before, 1,000 datasets of size n=49 were generated from the reported means, standard deviations, and correlations. For each replication, a structural equation model was fitted in which a latent exam factor, measured by Exams 2, 3, and 4, was regressed on the three self-regulated learning (SRL) module scores. Estimation was performed using robust maximum likelihood.

Code

sm_warning <- 0

structural_model_fit <- lapply(1:1e3, function(idx) {
  tryCatch(
    expr = {
      study_one_sim <- mvrnorm(n = 49, mu = means, Sigma = cov_matrix)
      
      study_one_sim <- pmax(pmin(study_one_sim, 100), 0)
      
      structural_model <- "
        Exam_Score =~ Exam_2 + Exam_3 + Exam_4
        Exam_Score ~ Module_1 + Module_2 + Module_3
      "
      
      sm_results <- sem(
        structural_model,
        data = as.data.frame(study_one_sim),
        estimator = "MLR"
      )
      
      sm_resid <- resid(sm_results, type = "cor")$cov
      sm_resid <- as.data.table(sm_resid[lower.tri(sm_resid)])
      
      sm_fit <- fitmeasures(sm_results,
                            c(
                              "chisq.scaled",
                              "cfi.robust",
                              "tli.robust",
                              "rmsea.robust"
                            )) |>
        as.data.table(keep.rownames = T)
      
      setnames(sm_fit, new = c("Fit Measure", "Value"))
      sm_fit[, `Fit Measure` := fcase(
        `Fit Measure` == "chisq.scaled",
        "Chi-Square",
        `Fit Measure` == "cfi.robust",
        "CFI",
        `Fit Measure` == "tli.robust",
        "TLI",
        `Fit Measure` == "rmsea.robust",
        "RMSEA"
      )]
      
      sm_parameters <- as.data.table(parameterestimates(sm_results))
      sm_parameters <- sm_parameters[op == "~"]
      
      return(list(residuals = sm_resid, model_fit = sm_fit, sm_parameters = sm_parameters))
    },
    warning = function (w) {
      mm_warning <<- sm_warning + 1
      return(NULL)
    },
    error = function (e) {
      return(NULL)
    }
  )
})

Across replications, global fit indices exhibited substantial variability. In some samples the structural model achieved excellent fit according to conventional criteria, whereas in others fit was clearly inadequate. This dispersion indicates that apparent model fit is highly sensitive to sampling variation at the observed sample size, limiting the inferential value of global fit statistics.

Code

Filter(Negate(is.null), lapply(structural_model_fit, function (x) x$model_fit)) |>
  rbindlist() |>
  ggplot(aes(Value)) +
  geom_histogram(colour = "black", fill = "white") +
  facet_wrap(~`Fit Measure`, scales = "free_x") +
  theme_bw()

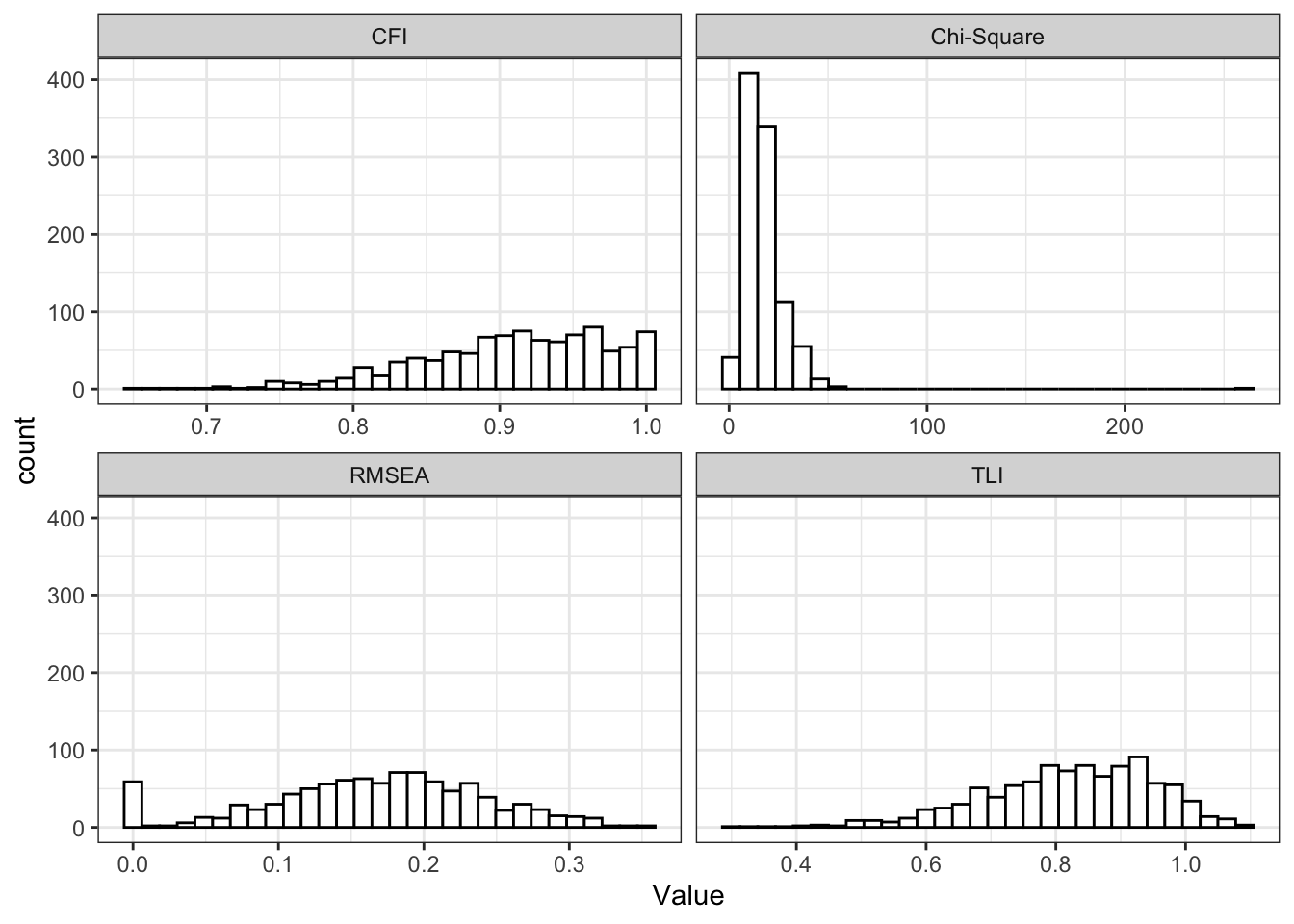
The estimated structural coefficients were small in magnitude and broadly consistent with those reported in the original study. However, across simulations these coefficients showed considerable dispersion, with wide sampling distributions and weak stability. In several replications, effects attenuated towards zero or varied in magnitude.

Code

Filter(Negate(is.null), lapply(structural_model_fit, function (x) x$sm_parameters)) |>
  rbindlist() |>
  ggplot(aes(x = est)) +
  geom_histogram(colour = "black", fill = "white") +
  facet_wrap(~rhs, scales = "free_x") +
  theme_bw()

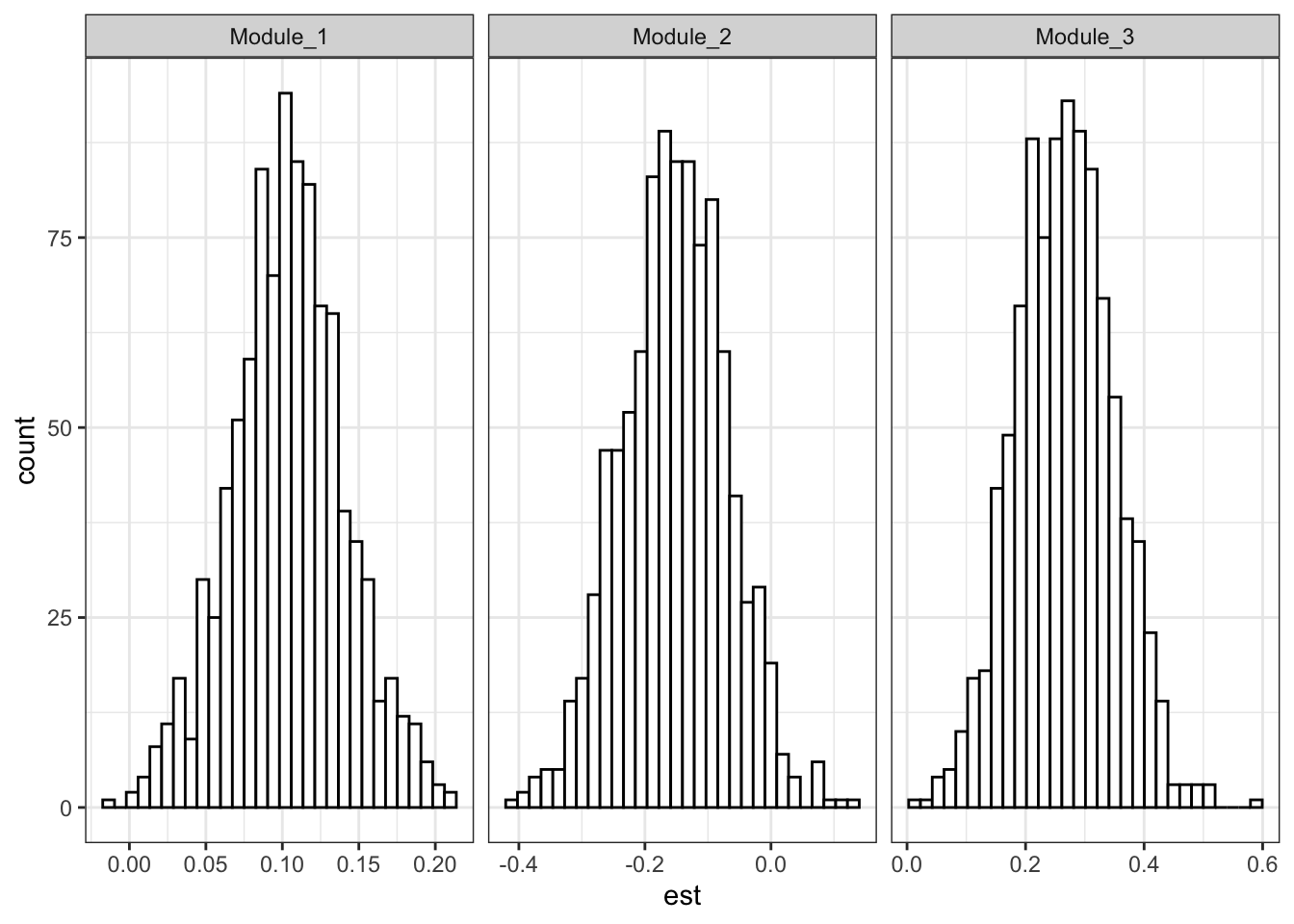
Taken together, these results indicate that even when the authors’ preferred latent structure is accepted for the sake of argument, the structural relations do not exhibit sufficient stability to support strong substantive claims. The combination of measurement instability, small sample size, and sensitivity of both fit indices and coefficients to sampling variation implies that the reported findings are compatible with chance variation under a flexible modelling framework. Consequently, the structural results should be interpreted as exploratory rather than as confirmatory evidence for selective effects of SRL components on exam performance.

Summary

This post does not propose an alternative model, nor does it challenge the theoretical relevance of self-regulated learning (SRL) constructs. Instead, it examines whether the statistical models used in the paper can support the strength of the conclusions drawn from them.

The results indicate that the proposed measurement model for exam performance is unstable and relies on assumptions that are unlikely to hold in the presence of temporally ordered, overlapping assessments. Residual dependence remains substantial, and apparent model fit is highly sensitive to sampling variation at the observed sample size. Even when the measurement model is accepted for the sake of argument, the structural model exhibits large variability in both global fit indices and coefficient estimates.

Taken together, these findings make the original conclusions difficult to reconcile with the evidential strength of the data. The results are compatible with chance variation under a flexible modelling framework applied to a small and selective sample. Future research would benefit from explicitly modelling dependency in repeated measures, strengthening measurement foundations, and ensuring sample sizes commensurate with model complexity.